from preamble import *
%matplotlib inline
Algorithm Chains and Pipelines¶
Content:
- Parameter Selection with Preprocessing
- Building Pipelines
- Using Pipelines in Grid Searches
- The General Pipeline Interface
- Convenient Pipeline Creation with make_pipeline
- Accessing Step Attributes
- Accessing Attributes in a Grid-Searched Pipeline
- Grid-Searching Preprocessing Steps and Model Parameters
- Grid-Searching Which Model To Use
- Summary and Outlook
In this chapter, we will cover how to use the Pipeline class to simplify the process of building chains of transformations and models. In particular, we will see how we can combine Pipeline and GridSearchCV to search over parameters for all processing steps at once.
As an example of the importance of chaining models, we noticed that we can greatly improve the performance of a kernel SVM on the cancer dataset by using the MinMaxScaler for preprocessing. Here’s code for splitting the data, computing the minimum and maximum, scaling the data, and training the SVM
from sklearn.svm import SVC
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# load and split the data
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
# compute minimum and maximum on the training data
scaler = MinMaxScaler().fit(X_train)
# rescale the training data
X_train_scaled = scaler.transform(X_train)
svm = SVC()
# learn an SVM on the scaled training data
svm.fit(X_train_scaled, y_train)
# scale the test data and score the scaled data
X_test_scaled = scaler.transform(X_test)
print("Test score: {:.2f}".format(svm.score(X_test_scaled, y_test)))
1. Parameter Selection with Preprocessing¶
from sklearn.model_selection import GridSearchCV
# for illustration purposes only, don't use this code!
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(SVC(), param_grid=param_grid, cv=5)
grid.fit(X_train_scaled, y_train)
print("Best cross-validation accuracy: {:.2f}".format(grid.best_score_))
print("Best parameters: ", grid.best_params_)
print("Test set accuracy: {:.2f}".format(grid.score(X_test_scaled, y_test)))
Here, we ran the grid search over the parameters of SVC using the scaled data.
- When scaling the data, we used all the data in the training set to find out how to train it.
- We then use the scaled training data to run our grid search using cross-validation.
Remember that the test part in each split in the cross-validation is part of the training set, and we used the information from the entire training set to find the right scaling of the data
- This is fundamentally different from how new data looks to the model.
- If we observe new data (say, in form of our test set), this data will not have been used to scale the training data, and it might have a different minimum and maximum than the training data.
mglearn.plots.plot_improper_processing()
The splitting of the dataset during cross-validation should be done before doing any preprocessing. Any process that extracts knowledge from the dataset should only ever be applied to the training portion of the dataset, so any cross-validation should be the “outermost loop” in your processing.
2. Building Pipelines¶
Using the pipeline, we reduced the code needed for our “preprocessing + classification” process.
from sklearn.pipeline import Pipeline
pipe = Pipeline([("scaler", MinMaxScaler()), ("svm", SVC())])
pipe.fit(X_train, y_train)
print("Test score: {:.2f}".format(pipe.score(X_test, y_test)))
As you can see, the result is identical to the one we got from the code at the beginning of the chapter, when doing the transformations by hand.
3. Using Pipelines in Grid-searches¶
param_grid = {'svm__C': [0.001, 0.01, 0.1, 1, 10, 100],
'svm__gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5)
grid.fit(X_train, y_train)
print("Best cross-validation accuracy: {:.2f}".format(grid.best_score_))
print("Test set score: {:.2f}".format(grid.score(X_test, y_test)))
print("Best parameters: {}".format(grid.best_params_))
mglearn.plots.plot_proper_processing()
Data usage when preprocessing inside the cross-validation loop with a pipeline
Information leakage is when information from a sealed system leaks out somewhere it shouldn’t.
Data leakage is simple any situation where a model gets access to information it otherwise wouldn’t know. For instance you might have data leakage because your model includes a particular feature that it wouldn’t otherwise ‘see.’
The impact of leaking information in the cross-validation varies depending on the nature of the preprocessing step. Estimating the scale of the data using the test fold usually doesn’t have a terrible impact, while using the test fold in feature extraction and feature selection can lead to substantial differences in outcomes.
rnd = np.random.RandomState(seed=0)
X = rnd.normal(size=(100, 10000))
y = rnd.normal(size=(100,))
from sklearn.feature_selection import SelectPercentile, f_regression
select = SelectPercentile(score_func=f_regression, percentile=5).fit(X, y)
X_selected = select.transform(X)
print("X_selected.shape: {}".format(X_selected.shape))
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import Ridge
print("Cross-validation accuracy (cv only on ridge): {:.2f}".format(
np.mean(cross_val_score(Ridge(), X_selected, y, cv=5))))
We fit the feature selection outside of the cross-validation, it could find features that are correlated both on the training and the test folds. The information we leaked from the test folds was very informative, leading to highly unrealistic results.
pipe = Pipeline([("select", SelectPercentile(score_func=f_regression,
percentile=5)),
("ridge", Ridge())])
print("Cross-validation accuracy (pipeline): {:.2f}".format(
np.mean(cross_val_score(pipe, X, y, cv=5))))
This time, we get a negative R-square score, indicating a very poor model. Using the pipeline, the feature selection is now inside the cross-validation loop. This means features can only be selected using the training folds of the data, not the test fold. The feature selection finds features that are correlated with the target on the training set, but because the data is entirely random, these features are not correlated with the target on the test set.
Note: Rectifying the data leakage issue in the feature selection makes the difference between concluding that a model works very well and concluding that a model works not at all.
4. The General Pipeline Interface¶
The Pipeline class is not restricted to preprocessing and classification, but can in fact join any number of estimators together. For example, you could build a pipeline containing feature extraction, feature selection, scaling, and classification, for a total of four steps.
def fit(self, X, y):
X_transformed = X
for name, estimator in self.steps[:-1]:
# iterate over all but the final step
# fit and transform the data
X_transformed = estimator.fit_transform(X_transformed, y)
# fit the last step
self.steps[-1][1].fit(X_transformed, y)
return self
def predict(self, X):
X_transformed = X
for step in self.steps[:-1]:
# iterate over all but the final step
# transform the data
X_transformed = step[1].transform(X_transformed)
# predict using the last step
return self.steps[-1][1].predict(X_transformed)
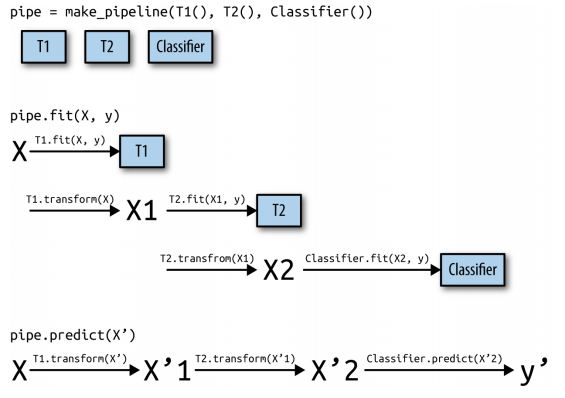
There is no requirement for the last step in a pipeline to have a predict function, and we could create a pipeline just containing, for example, a scaler and PCA.
4.1 Convenient Pipeline creation with make_pipeline¶
Creating a pipeline using the syntax described earlier is sometimes a bit cumbersome, and we often don’t need user-specified names for each step. There is a convenience function, make_pipeline, that will create a pipeline for us and automatically name each step based on its class.
from sklearn.pipeline import make_pipeline
# standard syntax
pipe_long = Pipeline([("scaler", MinMaxScaler()), ("svm", SVC(C=100))])
# abbreviated syntax
pipe_short = make_pipeline(MinMaxScaler(), SVC(C=100))
The pipeline objects pipe_long and pipe_short do exactly the same thing, but pipe_short has steps that were automatically named.
print("Pipeline steps:\n{}".format(pipe_short.steps))
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
pipe = make_pipeline(StandardScaler(), PCA(n_components=2), StandardScaler())
print("Pipeline steps:\n{}".format(pipe.steps))
4.2 Accessing step attributes¶
Often you will want to inspect (observe) attributes of one of the steps of the pipeline—say, the coefficients of a linear model or the components extracted by PCA. The easiest way to access the steps in a pipeline is via the named_steps attribute, which is a dictionary from the step names to the estimators
# fit the pipeline defined before to the cancer dataset
pipe.fit(cancer.data)
# extract the first two principal components from the "pca" step
components = pipe.named_steps["pca"].components_
print("components.shape: {}".format(components.shape))
4.3 Accessing Attributes in a Pipeline inside GridSearchCV¶
One of the main reasons to use pipelines is for doing grid searches. A common task is to access some of the steps of a pipeline inside a grid search.
from sklearn.linear_model import LogisticRegression
pipe = make_pipeline(StandardScaler(), LogisticRegression())
param_grid = {'logisticregression__C': [0.01, 0.1, 1, 10, 100]}
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=4)
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("Best estimator:\n{}".format(grid.best_estimator_))
print("Logistic regression step:\n{}".format(
grid.best_estimator_.named_steps["logisticregression"]))
print("Logistic regression coefficients:\n{}".format(
grid.best_estimator_.named_steps["logisticregression"].coef_))
5. Grid-searching preprocessing steps and model parameters¶
Using pipelines, we can encapsulate all the processing steps in our machine learning workflow in a single scikit-learn estimator.
Another benefit of doing this is that we can now adjust the parameters of the preprocessing using the outcome of a supervised task like regression or classification.
from sklearn.datasets import load_boston
boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target,
random_state=0)
from sklearn.preprocessing import PolynomialFeatures
pipe = make_pipeline(
StandardScaler(),
PolynomialFeatures(),
Ridge())
param_grid = {'polynomialfeatures__degree': [1, 2, 3],
'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
grid = GridSearchCV(pipe, param_grid=param_grid, cv=5, n_jobs=-1)
grid.fit(X_train, y_train)
mglearn.tools.heatmap(grid.cv_results_['mean_test_score'].reshape(3, -1),
xlabel="ridge__alpha", ylabel="polynomialfeatures__degree",
xticklabels=param_grid['ridge__alpha'],
yticklabels=param_grid['polynomialfeatures__degree'], vmin=0)
print("Best parameters: {}".format(grid.best_params_))
print("Test-set score: {:.2f}".format(grid.score(X_test, y_test)))
param_grid = {'ridge__alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
pipe = make_pipeline(StandardScaler(), Ridge())
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("Score without poly features: {:.2f}".format(grid.score(X_test, y_test)))
pipe = Pipeline([('preprocessing', StandardScaler()), ('classifier', SVC())])
from sklearn.ensemble import RandomForestClassifier
param_grid = [
{'classifier': [SVC()], 'preprocessing': [StandardScaler(), None],
'classifier__gamma': [0.001, 0.01, 0.1, 1, 10, 100],
'classifier__C': [0.001, 0.01, 0.1, 1, 10, 100]},
{'classifier': [RandomForestClassifier(n_estimators=100)],
'preprocessing': [None], 'classifier__max_features': [1, 2, 3]}]
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
grid = GridSearchCV(pipe, param_grid, cv=5)
grid.fit(X_train, y_train)
print("Best params:\n{}\n".format(grid.best_params_))
print("Best cross-validation score: {:.2f}".format(grid.best_score_))
print("Test-set score: {:.2f}".format(grid.score(X_test, y_test)))
Searching over preprocessing parameters together with model parameters is a very powerful strategy.
However, keep in mind that GridSearchCV tries all possible combinations of the specified parameters. Therefore, adding more parameters to your grid exponentially increases the number of models that need to be built.
6. Avoiding Redundant Computation¶
pipe = Pipeline([('preprocessing', StandardScaler()), ('classifier', SVC())],
memory="cache_folder")
7. Summary and Outlook¶
In this chapter
- We introduced the Pipeline class, a general-purpose tool to chain together multiple processing steps in a machine learning workflow. Real-world applications of machine learning rarely involve an isolated use of a model, and instead are a sequence of processing steps.
- In particular when doing model evaluation using crossvalidation and parameter selection using grid search, using the Pipeline class to capture all the processing steps is essential for proper evaluation. The Pipeline class also allows writing more succinct code, and reduces the likelihood of mistakes that can happen when building processing chains without the pipeline class (like forgetting to apply all transformers on the test set, or not applying them in the right order).
- Choosing the right combination of feature extraction, preprocessing, and models is somewhat of an art, and often requires some trial and error.
Comments !