from preamble import *
%matplotlib inline
Model Evaluation and Improvement¶
Content:
- Cross-Validation
- Cross-Validation in scikit-learn
- Benefits of Cross-Validation
- Stratified k-Fold Cross-Validation and Other Strategies
- Grid Search
- Simple Grid Search
- The Danger of Overfitting the Parameters and the Validation Set
- Grid Search with Cross-Validation
- Evaluation Metrics and Scoring
- Keep the End Goal in Mind
- Metrics for Binary Classification
- Metrics for Multiclass Classification
- Regression Metrics
- Using Evaluation Metrics in Model Selection
- Summary and Outlook
Model evaluation
- Model evaluation helps to find the best model that represents our data and how well the chosen model will work in the future.
- Evaluating model performance with the data used for training is not acceptable in data science because it can easily generate overoptimistic and overfitted models. (do not use training data to evaluate model)
- The performance of a model will be explain by evaluation metrics.
Evaluations metrics
- Evaluation metrics explain the performance of a model.
An important aspect of evaluation metrics is their capability to discriminate among model results.
Important Model Evaluation Metrics for Machine Learning
- Confusion Matrix
- F1 Score
- AUC – ROC
- Log Loss
- Root Mean Squared Error
- Cross Validation (Not a metric though!) ......
Remember, the reason we split our data into training and test sets is that we are interested in measuring how well our model generalizes to new, previously unseen data.
from sklearn.datasets import make_blobs
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# create a synthetic dataset
X, y = make_blobs(random_state=0)
# split data and labels into a training and a test set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# instantiate a model and fit it to the training set
logreg = LogisticRegression().fit(X_train, y_train)
# evaluate the model on the test set
print("Test set score: {:.2f}".format(logreg.score(X_test, y_test)))
1. Cross-Validation¶
Cross-validation is a statistical method of evaluating generalization performance that is more stable and thorough than using a split into a training and a test set.
In crossvalidation, the data is instead split repeatedly and multiple models are trained. The most commonly used version of cross-validation is k-fold cross-validation, where k is a user-specified number, usually 5 or 10.
mglearn.plots.plot_cross_validation()
- The first model is trained using the first fold as the test set, and the remaining folds (2–5) are used as the training set. The model is built using the data in folds 2–5, and then the accuracy is evaluated on fold 1.
- Another model is built, this time using fold 2 as the test set and the data in folds 1, 3, 4, and 5 as the training set.
This process is repeated using folds 3, 4, and 5 as test sets.
For each of these five splits of the data into training and test sets, we compute the accuracy. In the end, we have collected five accuracy values.
1.1 Cross-Validation in scikit-learn¶
from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
iris = load_iris()
logreg = LogisticRegression()
scores = cross_val_score(logreg, iris.data, iris.target)
print("Cross-validation scores: {}".format(scores))
scores = cross_val_score(logreg, iris.data, iris.target, cv=5)
print("Cross-validation scores: {}".format(scores))
Looking at all five scores produced by the five-fold cross-validation, we can also conclude that there is a relatively high variance in the accuracy between folds, ranging from 100% accuracy to 90% accuracy.
This could imply that the model is very dependent on the particular folds used for training, but it could also just be a consequence of the small size of the dataset.
print("Average cross-validation score: {:.2f}".format(scores.mean()))
A common way to summarize the cross-validation accuracy is to compute the mean¶
from sklearn.model_selection import cross_validate
res = cross_validate(logreg, iris.data, iris.target, cv=5,
return_train_score=True)
display(res)
res_df = pd.DataFrame(res)
display(res_df)
print("Mean times and scores:\n", res_df.mean())
1.2 Benefits of Cross-Validation¶
- Each example will be in the training set exactly once: each example is in one of the folds, and each fold is the test set once (instead of random split). Therefore, the model needs to generalize well to all of the samples in the dataset for all of the cross-validation scores (and their mean) to be high.
- Having multiple splits of the data also provides some information about how sensitive our model is to the selection of the training dataset
- Compared to using a single split of the data is that we use our data more effectively. Instead of using 75%-25% for train-test sets, we can use 80%(5-fold)-90%(10-fold) to fit the model and more data will usually result in more accurate models.
Note:
- The main disadvantage of cross-validation is increased computational cost. As we are now training k models instead of a single model, cross-validation will be roughly k-times slower than doing a single split of the data.
- It is important to keep in mind that cross-validation is not a way to build a model that can be applied to new data.
- Cross-validation does not return a model. When calling cross_val_score, multiple models are built internally, but the purpose of cross-validation is only to evaluate how well a given algorithm will generalize when trained on a specific dataset
1.3 Stratified K-Fold cross-validation and other strategies¶
As the simple k-fold strategy fails here, scikit-learn does not use it for classification, but rather uses stratified k-fold cross-validation.
- In stratified cross-validation, we split the data such that the proportions between classes are the same in each fold as they are in the whole dataset.
from sklearn.datasets import load_iris
iris = load_iris()
print("Iris labels:\n{}".format(iris.target))
mglearn.plots.plot_stratified_cross_validation()
In the case of only 10% of samples belonging each class. Using this fold as a test set would not be very informative about the overall performance of the classifier
More control over cross-validation¶
Another way to resolve this problem is to shuffle the data instead of stratifying the folds, to remove the ordering of the samples by label.
- We can do that by setting the shuffle parameter of KFold to True.
- If we shuffle the data, we also need to fix the random_state to get a reproducible shuffling.
- Otherwise, each run of cross_val_score would yield a different result, as each time a different split would be used (this might not be a problem, but can be surprising).
Shuffling the data before splitting it yields a much better result
from sklearn.model_selection import KFold
kfold = KFold(n_splits=5)
print("Cross-validation scores:\n{}".format(cross_val_score(logreg, iris.data, iris.target, cv=kfold)))
This way, we can verify that it is indeed a really bad idea to use three-fold (nonstratified) cross-validation on the iris dataset
kfold = KFold(n_splits=3)
print("Cross-validation scores:\n{}".format(
cross_val_score(logreg, iris.data, iris.target, cv=kfold)))
kfold = KFold(n_splits=3, shuffle=True, random_state=0)
print("Cross-validation scores:\n{}".format(
cross_val_score(logreg, iris.data, iris.target, cv=kfold)))
Leave-one-out cross-validation¶
leave-one-out cross-validation as k-fold cross-validation where each fold is a single sample.
- For each split, you pick a single data point to be the test set.
This can be very time consuming, particularly for large datasets, but sometimes provides better estimates on small datasets
from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
scores = cross_val_score(logreg, iris.data, iris.target, cv=loo)
print("Number of cv iterations: ", len(scores))
print("Mean accuracy: {:.2f}".format(scores.mean()))
Shuffle-split cross-validation¶
In shuffle-split cross-validation, each split samples train_size many points for the training set and test_size many (disjoint) point for the test set.
mglearn.plots.plot_shuffle_split()
from sklearn.model_selection import ShuffleSplit
shuffle_split = ShuffleSplit(test_size=.5, train_size=.5, n_splits=10)
scores = cross_val_score(logreg, iris.data, iris.target, cv=shuffle_split)
print("Cross-validation scores:\n{}".format(scores))
Cross-validation with groups¶
The goal is to build a classifier that can correctly identify a new class not in the dataset
- It will be much easier for a classifier to detect an exited object that is part of the training set, compared to a completely new object. To accurately evaluate the generalization to new object, we must therefore ensure that the training and test sets contain many different objects.
mglearn.plots.plot_group_kfold()
from sklearn.model_selection import GroupKFold
# create synthetic dataset
X, y = make_blobs(n_samples=12, random_state=0)
# assume the first three samples belong to the same group,
# then the next four, etc.
groups = [0, 0, 0, 1, 1, 1, 1, 2, 2, 3, 3, 3]
scores = cross_val_score(logreg, X, y, groups, cv=GroupKFold(n_splits=3))
print("Cross-validation scores:\n{}".format(scores))
2. Grid Search¶
- Tunning parameter is a important step to make model better.
Finding the values of the important parameters of a model (the ones that provide the best generalization performance) is a tricky task, but necessary for almost all models and datasets.
2.1 Simple Grid Search¶
We can implement a simple grid search just as for loops over the parameters(examples: gamma and C in SVC model), training and evaluating a classifier for each combination
# naive grid search implementation
from sklearn.svm import SVC
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=0)
print("Size of training set: {} size of test set: {}".format(
X_train.shape[0], X_test.shape[0]))
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters, train an SVC
svm = SVC(gamma=gamma, C=C)
svm.fit(X_train, y_train)
# evaluate the SVC on the test set
score = svm.score(X_test, y_test)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
print("Best score: {:.2f}".format(best_score))
print("Best parameters: {}".format(best_parameters))
The danger of overfitting the parameters and the validation set¶
- We tried many different parameters and selected the one with best accuracy on the test set, but this accuracy won’t necessarily carry over to new data. Because we used the test data to adjust the parameters, we can no longer use it to assess how good the model is. We need an independent dataset to evaluate, one that was not used to create the model.
mglearn.plots.plot_threefold_split()
After selecting the best parameters using the validation set, we can rebuild a model using the parameter settings we found, but now training on both the training data and the validation data
from sklearn.svm import SVC
# split data into train+validation set and test set
X_trainval, X_test, y_trainval, y_test = train_test_split(
iris.data, iris.target, random_state=0)
# split train+validation set into training and validation sets
X_train, X_valid, y_train, y_valid = train_test_split(
X_trainval, y_trainval, random_state=1)
print("Size of training set: {} size of validation set: {} size of test set:"
" {}\n".format(X_train.shape[0], X_valid.shape[0], X_test.shape[0]))
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters, train an SVC
svm = SVC(gamma=gamma, C=C)
svm.fit(X_train, y_train)
# evaluate the SVC on the validation set
score = svm.score(X_valid, y_valid)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
# rebuild a model on the combined training and validation set,
# and evaluate it on the test set
svm = SVC(**best_parameters)
svm.fit(X_trainval, y_trainval)
test_score = svm.score(X_test, y_test)
print("Best score on validation set: {:.2f}".format(best_score))
print("Best parameters: ", best_parameters)
print("Test set score with best parameters: {:.2f}".format(test_score))
Any choices made based on the test set accuracy “leak” information from the test set into the model.
=>Therefore, it is important to keep a separate test set, which is only used for the final evaluation. It is good practice to do all exploratory analysis and model selection using the combination of a training and a validation set, and reserve the test set for a final evaluation—this is even true for exploratory visualization
2.2 Grid Search with Cross-Validation¶
For a better estimate of the generalization performance, instead of using a single split into a training and a validation set, we can use cross-validation to evaluate the performance of each parameter combination.
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
# for each combination of parameters,
# train an SVC
svm = SVC(gamma=gamma, C=C)
# perform cross-validation
scores = cross_val_score(svm, X_trainval, y_trainval, cv=5)
# compute mean cross-validation accuracy
score = np.mean(scores)
# if we got a better score, store the score and parameters
if score > best_score:
best_score = score
best_parameters = {'C': C, 'gamma': gamma}
# rebuild a model on the combined training and validation set
svm = SVC(**best_parameters)
svm.fit(X_trainval, y_trainval)
mglearn.plots.plot_cross_val_selection()
For each parameter setting (only a subset is shown), five accuracy values are computed, one for each split in the cross-validation. Then the mean validation accuracy is computed for each parameter setting. The parameters with the highest mean validation accuracy are chosen, marked by the circle
mglearn.plots.plot_grid_search_overview()
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
print("Parameter grid:\n{}".format(param_grid))
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
grid_search = GridSearchCV(SVC(), param_grid, cv=5,
return_train_score=True)
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=0)
grid_search.fit(X_train, y_train)
print("Test set score: {:.2f}".format(grid_search.score(X_test, y_test)))
print("Best parameters: {}".format(grid_search.best_params_))
print("Best cross-validation score: {:.2f}".format(grid_search.best_score_))
print("Best estimator:\n{}".format(grid_search.best_estimator_))
Note:¶
- Cross-validation is a way to evaluate a given algorithm on a specific dataset. However, it is often used in conjunction with parameter search methods like grid search
2.3 Analyzing the result of cross-validation¶
It is often helpful to visualize the results of cross-validation, to understand how the model generalization depends on the parameters we are searching.
import pandas as pd
# convert to Dataframe
results = pd.DataFrame(grid_search.cv_results_)
# show the first 5 rows
display(results.head())
We can inspect(observe) the results of the cross-validated grid search, and possibly expand our search
scores = np.array(results.mean_test_score).reshape(6, 6)
# plot the mean cross-validation scores
mglearn.tools.heatmap(scores, xlabel='gamma', xticklabels=param_grid['gamma'],
ylabel='C', yticklabels=param_grid['C'], cmap="viridis")
Each point in the heat map corresponds to one run of cross-validation, with a particular parameter setting. The color encodes the cross-validation accuracy, with light colors meaning high accuracy and dark colors meaning low accuracy.
fig, axes = plt.subplots(1, 3, figsize=(13, 5))
param_grid_linear = {'C': np.linspace(1, 2, 6),
'gamma': np.linspace(1, 2, 6)}
param_grid_one_log = {'C': np.linspace(1, 2, 6),
'gamma': np.logspace(-3, 2, 6)}
param_grid_range = {'C': np.logspace(-3, 2, 6),
'gamma': np.logspace(-7, -2, 6)}
for param_grid, ax in zip([param_grid_linear, param_grid_one_log,
param_grid_range], axes):
grid_search = GridSearchCV(SVC(), param_grid, cv=5)
grid_search.fit(X_train, y_train)
scores = grid_search.cv_results_['mean_test_score'].reshape(6, 6)
# plot the mean cross-validation scores
scores_image = mglearn.tools.heatmap(
scores, xlabel='gamma', ylabel='C', xticklabels=param_grid['gamma'],
yticklabels=param_grid['C'], cmap="viridis", ax=ax)
plt.colorbar(scores_image, ax=axes.tolist())
The first panel shows no changes at all, with a constant color over the whole parameter grid. In this case, this is caused by improper scaling and range of the parameters C and gamma. However, if no change in accuracy => a parameter is just not important at all.
The second panel shows a vertical stripe pattern. This could mean that the gamma parameter is searching over interesting values but the C parameter is not—or it could mean the C parameter is not important.
The third panel shows changes in both C and gamma. We can expect that there might be even better values beyond this border, and we might want to change our search range to include more parameters in this region.
Note:
- Tuning the parameter grid based on the cross-validation scores is perfectly fine, and a good way to explore the importance of different parameters.
- You should not test different parameter ranges on the final test set—as we discussed earlier, evaluation of the test set should happen only once we know exactly what model we want to use.
param_grid = [{'kernel': ['rbf'],
'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]},
{'kernel': ['linear'],
'C': [0.001, 0.01, 0.1, 1, 10, 100]}]
print("List of grids:\n{}".format(param_grid))
grid_search = GridSearchCV(SVC(), param_grid, cv=5,
return_train_score=True)
grid_search.fit(X_train, y_train)
print("Best parameters: {}".format(grid_search.best_params_))
print("Best cross-validation score: {:.2f}".format(grid_search.best_score_))
results = pd.DataFrame(grid_search.cv_results_)
# we display the transposed table so that it better fits on the page:
display(results.T)
Using different cross-validation strategies with grid search¶
Nested cross-validation¶
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10, 100]}
scores = cross_val_score(GridSearchCV(SVC(), param_grid, cv=5),
iris.data, iris.target, cv=5)
print("Cross-validation scores: ", scores)
print("Mean cross-validation score: ", scores.mean())
def nested_cv(X, y, inner_cv, outer_cv, Classifier, parameter_grid):
outer_scores = []
# for each split of the data in the outer cross-validation
# (split method returns indices of training and test parts)
for training_samples, test_samples in outer_cv.split(X, y):
# find best parameter using inner cross-validation
best_parms = {}
best_score = -np.inf
# iterate over parameters
for parameters in parameter_grid:
# accumulate score over inner splits
cv_scores = []
# iterate over inner cross-validation
for inner_train, inner_test in inner_cv.split(
X[training_samples], y[training_samples]):
# build classifier given parameters and training data
clf = Classifier(**parameters)
clf.fit(X[inner_train], y[inner_train])
# evaluate on inner test set
score = clf.score(X[inner_test], y[inner_test])
cv_scores.append(score)
# compute mean score over inner folds
mean_score = np.mean(cv_scores)
if mean_score > best_score:
# if better than so far, remember parameters
best_score = mean_score
best_params = parameters
# build classifier on best parameters using outer training set
clf = Classifier(**best_params)
clf.fit(X[training_samples], y[training_samples])
# evaluate
outer_scores.append(clf.score(X[test_samples], y[test_samples]))
return np.array(outer_scores)
from sklearn.model_selection import ParameterGrid, StratifiedKFold
scores = nested_cv(iris.data, iris.target, StratifiedKFold(5),
StratifiedKFold(5), SVC, ParameterGrid(param_grid))
print("Cross-validation scores: {}".format(scores))
Parallelizing cross-validation and grid search¶
3. Evaluation Metrics and Scoring¶
- There are only two of the many possible ways to summarize how well a supervised model performs on a given dataset.
- Evaluations metrics:
- Evaluation metrics explain the performance of a model.
- An important aspect of evaluation metrics is their capability to discriminate among model results.
3.1 Keep the End Goal in Mind¶
- Determined the end goal of the machine learning application, not just in making accurate predictions.
When choosing a model or adjusting parameters, you should pick the model or parameter values that have the most positive influence on the business metric. Often this is hard, as assessing(evaluating) the business impact of a particular model might require putting it in production in a real-life system.
- We often need to find some surrogate evaluation procedure, using an evaluation metric that is easier to compute. Keep in mind that this is only a surrogate, and it pays off to find the closest metric to the original business goal that is feasible to evaluate. This closest metric should be used whenever possible for model evaluation and selection. The result of this evaluation might not be a single number, but it should capture the expected business impact of choosing one model over another
For each different problems, we need a metrics that is more and more suitable to evaluate our models.
3.2 Metrics for Binary Classification¶
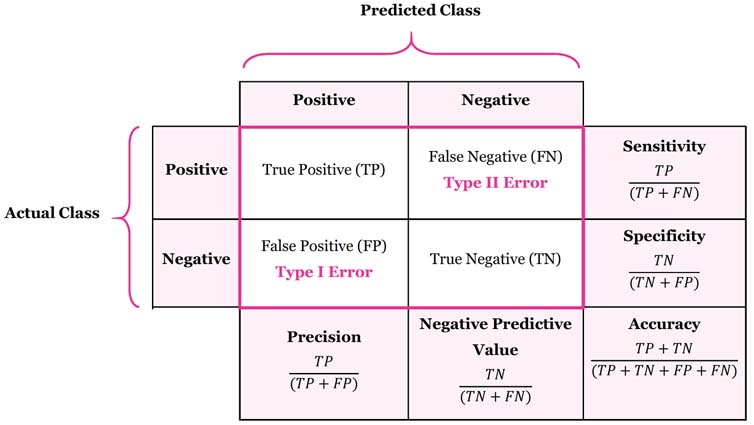
Remember that for binary classification, we often speak of a positive class and a negative class, with the understanding that the positive class is the one we are looking for.
Kinds of errors¶
Often, accuracy is not a good measure of predictive performance, as the number of mistakes we make does not contain all the information we are interested in.
Imagine an application to screen for the early detection of cancer using an automated test.
- If the test is negative, the patient will be assumed healthy => negative class
- If the test is positive, the patient will undergo additional screening => positive class
We can’t assume that our model will always work perfectly, and it will make mistakes => the consequences is
- An incorrect positive prediction is called a false positive, type I error
- An incorrect negative prediction is called a false negative, type II error
Imbalanced datasets¶
Datasets in which one class is much more frequent than the other are often called imbalanced datasets, or datasets with imbalanced classes. This is most common cause of error.
from sklearn.datasets import load_digits
digits = load_digits()
y = digits.target == 9
X_train, X_test, y_train, y_test = train_test_split(
digits.data, y, random_state=0)
from sklearn.dummy import DummyClassifier
dummy_majority = DummyClassifier(strategy='most_frequent').fit(X_train, y_train)
pred_most_frequent = dummy_majority.predict(X_test)
print("Unique predicted labels: {}".format(np.unique(pred_most_frequent)))
print("Test score: {:.2f}".format(dummy_majority.score(X_test, y_test)))
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=2).fit(X_train, y_train)
pred_tree = tree.predict(X_test)
print("Test score: {:.2f}".format(tree.score(X_test, y_test)))
from sklearn.linear_model import LogisticRegression
dummy = DummyClassifier().fit(X_train, y_train)
pred_dummy = dummy.predict(X_test)
print("dummy score: {:.2f}".format(dummy.score(X_test, y_test)))
logreg = LogisticRegression(C=0.1).fit(X_train, y_train)
pred_logreg = logreg.predict(X_test)
print("logreg score: {:.2f}".format(logreg.score(X_test, y_test)))
Confusion matrices¶
One of the most comprehensive ways to represent the result of evaluating binary classification is using confusion matrices.
A confusion matrix is an N X N matrix, where N is the number of classes being predicted. For the problem in hand (2 class), we have N=2, and hence we get a 2 X 2 matrix.
Confusion matrix is a performance measurement for machine learning classification problem where output can be two or more classes.
from sklearn.metrics import confusion_matrix
confusion = confusion_matrix(y_test, pred_logreg)
print("Confusion matrix:\n{}".format(confusion))
mglearn.plots.plot_confusion_matrix_illustration()
mglearn.plots.plot_binary_confusion_matrix()
print("Most frequent class:")
print(confusion_matrix(y_test, pred_most_frequent))
print("\nDummy model:")
print(confusion_matrix(y_test, pred_dummy))
print("\nDecision tree:")
print(confusion_matrix(y_test, pred_tree))
print("\nLogistic Regression")
print(confusion_matrix(y_test, pred_logreg))
Relation to accuracy¶
- Accuracy is the number of correct predictions (TP and TN) divided
by the number of all samples (all entries of the confusion matrix summed up)
\begin{equation}
\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}}
\end{equation}
Accuracy:
- Accuracy is used when the True Positives and True negatives are more important
- Accuracy can be used when the class distribution is similar. Accuracy is most used when all the classes are equally important.
Precision, recall and f-score¶
Precision:
Precision measures how many of the samples predicted as positive are actually positive.
- The proportion of positive cases that were correctly identified.
Ex: Fire alarm prediction
Recall:
Measures how many of the positive samples are captured by the positive predictions Recall is used as performance metric when we need to identify all positive samples;that is, when it is important to avoid false negatives.
- The proportion of actual positive cases which are correctly identified. \begin{equation} \text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} \end{equation} Other names for recall are sensitivity
For a given class, the different combinations of recall and precision have the following meanings :
- high recall + high precision : the class is perfectly handled by the model
- low recall + high precision : the model can’t detect the class well but is highly trustable when it does
- high recall + low precision : the class is well detected but the model also include points of other classes in it
- low recall + low precision : the class is poorly handled by the model
F1-score:
- F1-score is the harmonic mean of precision and recall values for a classification problems.
- F1-score gives a better measure of the incorrectly classified cases than the Accuracy Metric.
- F1-score is used when the False Negatives and False Positives are crucial(important).
- F1-score is a better metric when there are imbalanced classes. \begin{equation} \text{F1} = 2 \cdot \frac{\text{precision} \cdot \text{recall}}{\text{precision} + \text{recall}} \end{equation}

from sklearn.metrics import f1_score
print("f1 score most frequent: {:.2f}".format(
f1_score(y_test, pred_most_frequent)))
print("f1 score dummy: {:.2f}".format(f1_score(y_test, pred_dummy)))
print("f1 score tree: {:.2f}".format(f1_score(y_test, pred_tree)))
print("f1 score logistic regression: {:.2f}".format(
f1_score(y_test, pred_logreg)))
from sklearn.metrics import classification_report
print(classification_report(y_test, pred_most_frequent,
target_names=["not nine", "nine"]))
print(classification_report(y_test, pred_dummy,
target_names=["not nine", "nine"]))
print(classification_report(y_test, pred_logreg,
target_names=["not nine", "nine"]))
Taking uncertainty into account¶
X, y = make_blobs(n_samples=(400, 50), cluster_std=[7.0, 2],
random_state=22)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
svc = SVC(gamma=.05).fit(X_train, y_train)
mglearn.plots.plot_decision_threshold()
print(classification_report(y_test, svc.predict(X_test)))
y_pred_lower_threshold = svc.decision_function(X_test) > -.8
print(classification_report(y_test, y_pred_lower_threshold))
Precision-Recall curves and ROC curves¶
from sklearn.metrics import precision_recall_curve
precision, recall, thresholds = precision_recall_curve(
y_test, svc.decision_function(X_test))
# Use more data points for a smoother curve
X, y = make_blobs(n_samples=(4000, 500), cluster_std=[7.0, 2], random_state=22)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
svc = SVC(gamma=.05).fit(X_train, y_train)
precision, recall, thresholds = precision_recall_curve(
y_test, svc.decision_function(X_test))
# find threshold closest to zero
close_zero = np.argmin(np.abs(thresholds))
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.plot(precision, recall, label="precision recall curve")
plt.xlabel("Precision")
plt.ylabel("Recall")
plt.legend(loc="best")
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100, random_state=0, max_features=2)
rf.fit(X_train, y_train)
# RandomForestClassifier has predict_proba, but not decision_function
precision_rf, recall_rf, thresholds_rf = precision_recall_curve(
y_test, rf.predict_proba(X_test)[:, 1])
plt.plot(precision, recall, label="svc")
plt.plot(precision[close_zero], recall[close_zero], 'o', markersize=10,
label="threshold zero svc", fillstyle="none", c='k', mew=2)
plt.plot(precision_rf, recall_rf, label="rf")
close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5))
plt.plot(precision_rf[close_default_rf], recall_rf[close_default_rf], '^', c='k',
markersize=10, label="threshold 0.5 rf", fillstyle="none", mew=2)
plt.xlabel("Precision")
plt.ylabel("Recall")
plt.legend(loc="best")
print("f1_score of random forest: {:.3f}".format(
f1_score(y_test, rf.predict(X_test))))
print("f1_score of svc: {:.3f}".format(f1_score(y_test, svc.predict(X_test))))
from sklearn.metrics import average_precision_score
ap_rf = average_precision_score(y_test, rf.predict_proba(X_test)[:, 1])
ap_svc = average_precision_score(y_test, svc.decision_function(X_test))
print("Average precision of random forest: {:.3f}".format(ap_rf))
print("Average precision of svc: {:.3f}".format(ap_svc))
Receiver Operating Characteristics (ROC) and AUC¶
\begin{equation} \text{FPR} = \frac{\text{FP}}{\text{FP} + \text{TN}} \end{equation}from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_test, svc.decision_function(X_test))
plt.plot(fpr, tpr, label="ROC Curve")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
# find threshold closest to zero
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
label="threshold zero", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
fpr_rf, tpr_rf, thresholds_rf = roc_curve(y_test, rf.predict_proba(X_test)[:, 1])
plt.plot(fpr, tpr, label="ROC Curve SVC")
plt.plot(fpr_rf, tpr_rf, label="ROC Curve RF")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10,
label="threshold zero SVC", fillstyle="none", c='k', mew=2)
close_default_rf = np.argmin(np.abs(thresholds_rf - 0.5))
plt.plot(fpr_rf[close_default_rf], tpr[close_default_rf], '^', markersize=10,
label="threshold 0.5 RF", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)
from sklearn.metrics import roc_auc_score
rf_auc = roc_auc_score(y_test, rf.predict_proba(X_test)[:, 1])
svc_auc = roc_auc_score(y_test, svc.decision_function(X_test))
print("AUC for Random Forest: {:.3f}".format(rf_auc))
print("AUC for SVC: {:.3f}".format(svc_auc))
y = digits.target == 9
X_train, X_test, y_train, y_test = train_test_split(
digits.data, y, random_state=0)
plt.figure()
for gamma in [1, 0.05, 0.01]:
svc = SVC(gamma=gamma).fit(X_train, y_train)
accuracy = svc.score(X_test, y_test)
auc = roc_auc_score(y_test, svc.decision_function(X_test))
fpr, tpr, _ = roc_curve(y_test , svc.decision_function(X_test))
print("gamma = {:.2f} accuracy = {:.2f} AUC = {:.2f}".format(
gamma, accuracy, auc))
plt.plot(fpr, tpr, label="gamma={:.3f}".format(gamma))
plt.xlabel("FPR")
plt.ylabel("TPR")
plt.xlim(-0.01, 1)
plt.ylim(0, 1.02)
plt.legend(loc="best")
3.3 Metrics for Multiclass Classification¶
Apart from accuracy, common tools are the confusion matrix and the classification report we saw in the binary case in the previous section.
from sklearn.metrics import accuracy_score
X_train, X_test, y_train, y_test = train_test_split(
digits.data, digits.target, random_state=0)
lr = LogisticRegression().fit(X_train, y_train)
pred = lr.predict(X_test)
print("Accuracy: {:.3f}".format(accuracy_score(y_test, pred)))
print("Confusion matrix:\n{}".format(confusion_matrix(y_test, pred)))
- The model has an accuracy of 95.3%, which already tells us that we are doing pretty well.
- The confusion matrix provides us with some more detail. As for the binary case, each row corresponds to a true label, and each column corresponds to a predicted label.
scores_image = mglearn.tools.heatmap(
confusion_matrix(y_test, pred), xlabel='Predicted label',
ylabel='True label', xticklabels=digits.target_names,
yticklabels=digits.target_names, cmap=plt.cm.gray_r, fmt="%d")
plt.title("Confusion matrix")
plt.gca().invert_yaxis()
print(classification_report(y_test, pred))
The most commonly used metric for imbalanced datasets in the multiclass setting is the multiclass version of the f-score.
The idea behind the multiclass f-score is to compute one binary f-score per class, with that class being the positive class and the other classes making up the negative classes.¶
Then, these perclass f-scores are averaged using one of the following strategies:
- "macro" averaging computes the unweighted per-class f-scores. This gives equal weight to all classes, no matter what their size is.
- "weighted" averaging computes the mean of the per-class f-scores, weighted by their support. This is what is reported in the classification report.
- "micro" averaging computes the total number of false positives, false negatives, and true positives over all classes, and then computes precision, recall, and fscore using these counts.
- If you care about each sample equally much, it is recommended to use the "micro" average f1 -score;
- if you care about each class equally much, it is recommended to use the "macro" average f1 -score
print("Micro average f1 score: {:.3f}".format(
f1_score(y_test, pred, average="micro")))
print("Macro average f1 score: {:.3f}".format(
f1_score(y_test, pred, average="macro")))
3.4 Regression metrics¶
In most applications we’ve seen, using the default R-square used in the score method of all regressors is enough.
Sometimes business decisions are made on the basis of mean squared error or mean absolute error, which might give incentive to tune models using these metrics.
R-squared (R2)
- A statistical measure that represents the proportion of the variance for a dependent variable that's explained by an independent variable or variables in a regression model.
In a way, R-squared measures how much prediction error is eliminated when we use least-squares regression.
- R-squared tells us what percent of the prediction error in the y variable is eliminated when we use least-squares regression on the x variable. R-squared is also called the coefficient of determination.
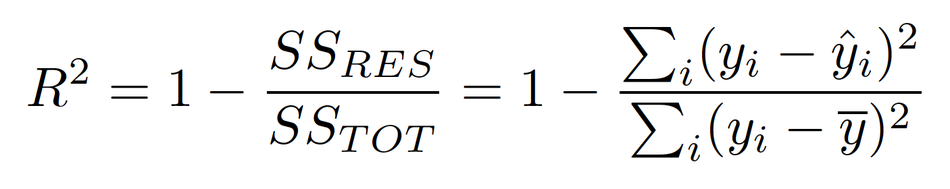
- If the R2 of a model is 0.50, then approximately half of the observed variation can be explained by the model's inputs.
Root mean square error (RMSE):
- RMSE is a frequently used measure of the differences between values predicted by a model or an estimator and the values observed.
- RMSE is the most popular evaluation metric used in regression problems.
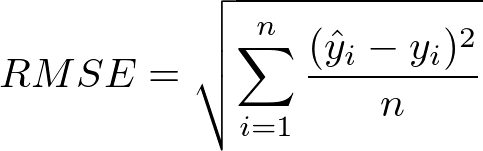
Using evaluation metrics in model selection¶
# default scoring for classification is accuracy
print("Default scoring: {}".format(
cross_val_score(SVC(), digits.data, digits.target == 9, cv=5)))
# providing scoring="accuracy" doesn't change the results
explicit_accuracy = cross_val_score(SVC(), digits.data, digits.target == 9,
scoring="accuracy", cv=5)
print("Explicit accuracy scoring: {}".format(explicit_accuracy))
roc_auc = cross_val_score(SVC(), digits.data, digits.target == 9,
scoring="roc_auc", cv=5)
print("AUC scoring: {}".format(roc_auc))
res = cross_validate(SVC(), digits.data, digits.target == 9,
scoring=["accuracy", "roc_auc", "recall_macro"],
return_train_score=True, cv=5)
display(pd.DataFrame(res))
X_train, X_test, y_train, y_test = train_test_split(
digits.data, digits.target == 9, random_state=0)
# we provide a somewhat bad grid to illustrate the point:
param_grid = {'gamma': [0.0001, 0.01, 0.1, 1, 10]}
# using the default scoring of accuracy:
grid = GridSearchCV(SVC(), param_grid=param_grid)
grid.fit(X_train, y_train)
print("Grid-Search with accuracy")
print("Best parameters:", grid.best_params_)
print("Best cross-validation score (accuracy)): {:.3f}".format(grid.best_score_))
print("Test set AUC: {:.3f}".format(
roc_auc_score(y_test, grid.decision_function(X_test))))
print("Test set accuracy: {:.3f}".format(grid.score(X_test, y_test)))
# using AUC scoring instead:
grid = GridSearchCV(SVC(), param_grid=param_grid, scoring="roc_auc")
grid.fit(X_train, y_train)
print("\nGrid-Search with AUC")
print("Best parameters:", grid.best_params_)
print("Best cross-validation score (AUC): {:.3f}".format(grid.best_score_))
print("Test set AUC: {:.3f}".format(
roc_auc_score(y_test, grid.decision_function(X_test))))
print("Test set accuracy: {:.3f}".format(grid.score(X_test, y_test)))
from sklearn.metrics.scorer import SCORERS
print("Available scorers:")
print(sorted(SCORERS.keys()))
Summary and Outlook¶
- Cross-validation or the use of a test set allow us to evaluate a machine learning model as it will perform in the future
- The second point has to do with the importance of the evaluation metric or scoring function used for model selection and model evaluation
Comments !