%matplotlib inline
from preamble import *

import os
# The file has no headers naming the columns, so we pass header=None
# and provide the column names explicitly in "names"
adult_path = os.path.join(mglearn.datasets.DATA_PATH, "adult.data")
data = pd.read_csv(
    adult_path, header=None, index_col=False,
    names=['age', 'workclass', 'fnlwgt', 'education',  'education-num',
           'marital-status', 'occupation', 'relationship', 'race', 'gender',
           'capital-gain', 'capital-loss', 'hours-per-week', 'native-country',
           'income'])
# For illustration purposes, we only select some of the columns
data = data[['age', 'workclass', 'education', 'gender', 'hours-per-week',
             'occupation', 'income']]
# IPython.display allows nice output formatting within the Jupyter notebook
display(data.head())

print(data.gender.value_counts())

print("Original features:\n", list(data.columns), "\n")
data_dummies = pd.get_dummies(data)
print("Features after get_dummies:\n", list(data_dummies.columns))

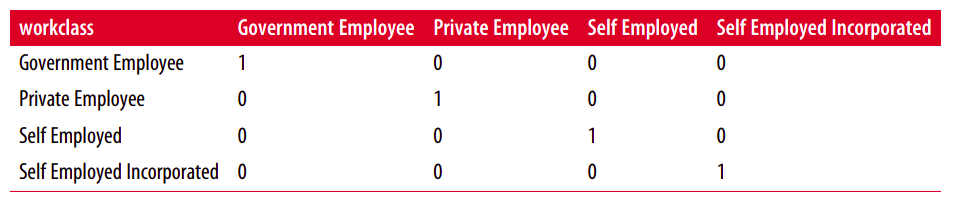
display(data_dummies.head())

features = data_dummies.loc[:, 'age':'occupation_ Transport-moving']
# Extract NumPy arrays
X = features.values
y = data_dummies['income_ >50K'].values
print("X.shape: {}  y.shape: {}".format(X.shape, y.shape))

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
print("Test score: {:.2f}".format(logreg.score(X_test, y_test)))

# create a DataFrame with an integer feature and a categorical string feature
demo_df = pd.DataFrame({'Integer Feature': [0, 1, 2, 1],
                        'Categorical Feature': ['socks', 'fox', 'socks', 'box']})
display(demo_df)

display(pd.get_dummies(demo_df))

demo_df['Integer Feature'] = demo_df['Integer Feature'].astype(str)
display(pd.get_dummies(demo_df, columns=['Integer Feature', 'Categorical Feature']))

from sklearn.preprocessing import OneHotEncoder
# Setting sparse=False means OneHotEncode will return a numpy array, not a sparse matrix
ohe = OneHotEncoder(sparse=False)
print(ohe.fit_transform(demo_df))

print(ohe.get_feature_names())

display(data.head())

from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import StandardScaler

ct = ColumnTransformer(
    [("scaling", StandardScaler(), ['age', 'hours-per-week']),
     ("onehot", OneHotEncoder(sparse=False), ['workclass', 'education', 'gender', 'occupation'])])

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
# get all columns apart from income for the features
data_features = data.drop("income", axis=1)
# split dataframe and income
X_train, X_test, y_train, y_test = train_test_split(
    data_features, data.income, random_state=0)

ct.fit(X_train)
X_train_trans = ct.transform(X_train)
print(X_train_trans.shape)

logreg = LogisticRegression()
logreg.fit(X_train_trans, y_train)

X_test_trans = ct.transform(X_test)
print("Test score: {:.2f}".format(logreg.score(X_test_trans, y_test)))

ct.named_transformers_.onehot

from sklearn.compose import make_column_transformer
ct = make_column_transformer(
    (['age', 'hours-per-week'], StandardScaler()),
    (['workclass', 'education', 'gender', 'occupation'], OneHotEncoder(sparse=False)))

from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor

X, y = mglearn.datasets.make_wave(n_samples=120)
line = np.linspace(-3, 3, 1000, endpoint=False).reshape(-1, 1)

reg = DecisionTreeRegressor(min_samples_leaf=3).fit(X, y)
plt.plot(line, reg.predict(line), label="decision tree")

reg = LinearRegression().fit(X, y)
plt.plot(line, reg.predict(line), label="linear regression")

plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")

from sklearn.preprocessing import KBinsDiscretizer

kb = KBinsDiscretizer(n_bins=10, strategy='uniform')
kb.fit(X)
print("bin edges: \n", kb.bin_edges_)

X_binned = kb.transform(X)
X_binned

print(X[:10])
X_binned.toarray()[:10]

kb = KBinsDiscretizer(n_bins=10, strategy='uniform', encode='onehot-dense')
kb.fit(X)
X_binned = kb.transform(X)

line_binned = kb.transform(line)

reg = LinearRegression().fit(X_binned, y)
plt.plot(line, reg.predict(line_binned), label='linear regression binned')

reg = DecisionTreeRegressor(min_samples_split=3).fit(X_binned, y)
plt.plot(line, reg.predict(line_binned), label='decision tree binned')
plt.plot(X[:, 0], y, 'o', c='k')
plt.vlines(kb.bin_edges_[0], -3, 3, linewidth=1, alpha=.2)
plt.legend(loc="best")
plt.ylabel("Regression output")
plt.xlabel("Input feature")

X_combined = np.hstack([X, X_binned])
print(X_combined.shape)

reg = LinearRegression().fit(X_combined, y)

line_combined = np.hstack([line, line_binned])
plt.plot(line, reg.predict(line_combined), label='linear regression combined')

plt.vlines(kb.bin_edges_[0], -3, 3, linewidth=1, alpha=.2)
plt.legend(loc="best")
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.plot(X[:, 0], y, 'o', c='k')

X_product = np.hstack([X_binned, X * X_binned])
print(X_product.shape)

reg = LinearRegression().fit(X_product, y)

line_product = np.hstack([line_binned, line * line_binned])
plt.plot(line, reg.predict(line_product), label='linear regression product')

plt.vlines(kb.bin_edges_[0], -3, 3, linewidth=1, alpha=.2)

plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")

from sklearn.preprocessing import PolynomialFeatures

# include polynomials up to x ** 10:
# the default "include_bias=True" adds a feature that's constantly 1
poly = PolynomialFeatures(degree=10, include_bias=False)
poly.fit(X)
X_poly = poly.transform(X)

print("X_poly.shape: {}".format(X_poly.shape))

print("Entries of X:\n{}".format(X[:5]))
print("Entries of X_poly:\n{}".format(X_poly[:5]))

print("Polynomial feature names:\n{}".format(poly.get_feature_names()))

reg = LinearRegression().fit(X_poly, y)

line_poly = poly.transform(line)
plt.plot(line, reg.predict(line_poly), label='polynomial linear regression')
plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")

from sklearn.svm import SVR

for gamma in [1, 10]:
    svr = SVR(gamma=gamma).fit(X, y)
    plt.plot(line, svr.predict(line), label='SVR gamma={}'.format(gamma))

plt.plot(X[:, 0], y, 'o', c='k')
plt.ylabel("Regression output")
plt.xlabel("Input feature")
plt.legend(loc="best")

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler

boston = load_boston()
X_train, X_test, y_train, y_test = train_test_split(
    boston.data, boston.target, random_state=0)

# rescale data
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

poly = PolynomialFeatures(degree=2).fit(X_train_scaled)
X_train_poly = poly.transform(X_train_scaled)
X_test_poly = poly.transform(X_test_scaled)
print("X_train.shape: {}".format(X_train.shape))
print("X_train_poly.shape: {}".format(X_train_poly.shape))

print("Polynomial feature names:\n{}".format(poly.get_feature_names()))

from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train_scaled, y_train)
print("Score without interactions: {:.3f}".format(
    ridge.score(X_test_scaled, y_test)))
ridge = Ridge().fit(X_train_poly, y_train)
print("Score with interactions: {:.3f}".format(
    ridge.score(X_test_poly, y_test)))

from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor(n_estimators=100).fit(X_train_scaled, y_train)
print("Score without interactions: {:.3f}".format(
    rf.score(X_test_scaled, y_test)))
rf = RandomForestRegressor(n_estimators=100).fit(X_train_poly, y_train)
print("Score with interactions: {:.3f}".format(rf.score(X_test_poly, y_test)))

rnd = np.random.RandomState(0)
X_org = rnd.normal(size=(1000, 3))
w = rnd.normal(size=3)

X = rnd.poisson(10 * np.exp(X_org))
y = np.dot(X_org, w)

print("Number of feature appearances:\n{}".format(np.bincount(X[:, 0])))

bins = np.bincount(X[:, 0])
plt.bar(range(len(bins)), bins, color='grey')
plt.ylabel("Number of appearances")
plt.xlabel("Value")

from sklearn.linear_model import Ridge
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
score = Ridge().fit(X_train, y_train).score(X_test, y_test)
print("Test score: {:.3f}".format(score))

X_train_log = np.log(X_train + 1)
X_test_log = np.log(X_test + 1)

plt.hist(X_train_log[:, 0], bins=25, color='gray')
plt.ylabel("Number of appearances")
plt.xlabel("Value")

score = Ridge().fit(X_train_log, y_train).score(X_test_log, y_test)
print("Test score: {:.3f}".format(score))

from sklearn.datasets import load_breast_cancer
from sklearn.feature_selection import SelectPercentile
from sklearn.model_selection import train_test_split

cancer = load_breast_cancer()

# get deterministic random numbers
rng = np.random.RandomState(42)
noise = rng.normal(size=(len(cancer.data), 50))
# add noise features to the data
# the first 30 features are from the dataset, the next 50 are noise
X_w_noise = np.hstack([cancer.data, noise])

X_train, X_test, y_train, y_test = train_test_split(
    X_w_noise, cancer.target, random_state=0, test_size=.5)
# use f_classif (the default) and SelectPercentile to select 50% of features
select = SelectPercentile(percentile=50)
select.fit(X_train, y_train)
# transform training set
X_train_selected = select.transform(X_train)

print("X_train.shape: {}".format(X_train.shape))
print("X_train_selected.shape: {}".format(X_train_selected.shape))

mask = select.get_support()
print(mask)
# visualize the mask. black is True, white is False
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
plt.xlabel("Sample index")
plt.yticks(())

from sklearn.linear_model import LogisticRegression

# transform test data
X_test_selected = select.transform(X_test)

lr = LogisticRegression()
lr.fit(X_train, y_train)
print("Score with all features: {:.3f}".format(lr.score(X_test, y_test)))
lr.fit(X_train_selected, y_train)
print("Score with only selected features: {:.3f}".format(
    lr.score(X_test_selected, y_test)))

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import RandomForestClassifier
select = SelectFromModel(
    RandomForestClassifier(n_estimators=100, random_state=42),
    threshold="median")

select.fit(X_train, y_train)
X_train_l1 = select.transform(X_train)
print("X_train.shape: {}".format(X_train.shape))
print("X_train_l1.shape: {}".format(X_train_l1.shape))

mask = select.get_support()
# visualize the mask. black is True, white is False
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
plt.xlabel("Sample index")
plt.yticks(())

X_test_l1 = select.transform(X_test)
score = LogisticRegression().fit(X_train_l1, y_train).score(X_test_l1, y_test)
print("Test score: {:.3f}".format(score))

from sklearn.feature_selection import RFE
select = RFE(RandomForestClassifier(n_estimators=100, random_state=42),
             n_features_to_select=40)

select.fit(X_train, y_train)
# visualize the selected features:
mask = select.get_support()
plt.matshow(mask.reshape(1, -1), cmap='gray_r')
plt.xlabel("Sample index")
plt.yticks(())

X_train_rfe = select.transform(X_train)
X_test_rfe = select.transform(X_test)

score = LogisticRegression().fit(X_train_rfe, y_train).score(X_test_rfe, y_test)
print("Test score: {:.3f}".format(score))

print("Test score: {:.3f}".format(select.score(X_test, y_test)))

citibike = mglearn.datasets.load_citibike()

print("Citi Bike data:\n{}".format(citibike.head()))

plt.figure(figsize=(10, 3))
xticks = pd.date_range(start=citibike.index.min(), end=citibike.index.max(),
                       freq='D')
plt.xticks(xticks, xticks.strftime("%a %m-%d"), rotation=90, ha="left")
plt.plot(citibike, linewidth=1)
plt.xlabel("Date")
plt.ylabel("Rentals")

# extract the target values (number of rentals)
y = citibike.values
# convert to POSIX time by dividing by 10**9
X = citibike.index.astype("int64").values.reshape(-1, 1) // 10**9

# use the first 184 data points for training, the rest for testing
n_train = 184

# function to evaluate and plot a regressor on a given feature set
def eval_on_features(features, target, regressor):
    # split the given features into a training and a test set
    X_train, X_test = features[:n_train], features[n_train:]
    # also split the target array
    y_train, y_test = target[:n_train], target[n_train:]
    regressor.fit(X_train, y_train)
    print("Test-set R^2: {:.2f}".format(regressor.score(X_test, y_test)))
    y_pred = regressor.predict(X_test)
    y_pred_train = regressor.predict(X_train)
    plt.figure(figsize=(10, 3))

    plt.xticks(range(0, len(X), 8), xticks.strftime("%a %m-%d"), rotation=90,
               ha="left")

    plt.plot(range(n_train), y_train, label="train")
    plt.plot(range(n_train, len(y_test) + n_train), y_test, '-', label="test")
    plt.plot(range(n_train), y_pred_train, '--', label="prediction train")

    plt.plot(range(n_train, len(y_test) + n_train), y_pred, '--',
             label="prediction test")
    plt.legend(loc=(1.01, 0))
    plt.xlabel("Date")
    plt.ylabel("Rentals")

from sklearn.ensemble import RandomForestRegressor
regressor = RandomForestRegressor(n_estimators=100, random_state=0)
eval_on_features(X, y, regressor)

X_hour = citibike.index.hour.values.reshape(-1, 1)
eval_on_features(X_hour, y, regressor)

X_hour_week = np.hstack([citibike.index.dayofweek.values.reshape(-1, 1),
                         citibike.index.hour.values.reshape(-1, 1)])
eval_on_features(X_hour_week, y, regressor)

from sklearn.linear_model import LinearRegression
eval_on_features(X_hour_week, y, LinearRegression())

enc = OneHotEncoder()
X_hour_week_onehot = enc.fit_transform(X_hour_week).toarray()

eval_on_features(X_hour_week_onehot, y, Ridge())

poly_transformer = PolynomialFeatures(degree=2, interaction_only=True,
                                      include_bias=False)
X_hour_week_onehot_poly = poly_transformer.fit_transform(X_hour_week_onehot)
lr = Ridge()
eval_on_features(X_hour_week_onehot_poly, y, lr)

hour = ["%02d:00" % i for i in range(0, 24, 3)]
day = ["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"]
features =  day + hour

features_poly = poly_transformer.get_feature_names(features)
features_nonzero = np.array(features_poly)[lr.coef_ != 0]
coef_nonzero = lr.coef_[lr.coef_ != 0]

plt.figure(figsize=(15, 2))
plt.plot(coef_nonzero, 'o')
plt.xticks(np.arange(len(coef_nonzero)), features_nonzero, rotation=90)
plt.xlabel("Feature name")
plt.ylabel("Feature magnitude")