%matplotlib inline
from preamble import *
plt.rcParams['image.cmap'] = "gray"
Unsupervised Learning¶
Content¶
- Unsupervised Learning and Preprocessing
- Types of Unsupervised Learning
- Challenges in Unsupervised Learning
- Preprocessing and Scaling
- Different Kinds of Preprocessing
- Applying Data Transformations
- Scaling Training and Test Data the Same Way
- The Effect of Preprocessing on Supervised Learning
- Dimensionality Reduction, Feature Extraction, and Manifold Learning
- Principal Component Analysis (PCA)
- Non-Negative Matrix Factorization (NMF)
- Manifold Learning with t-SNE
- Clustering 168
- k-Means Clustering
- Agglomerative Clustering
- DBSCAN
- Comparing and Evaluating Clustering Algorithms
- Summary of Clustering Methods
- Summary and Outlook
1. Unsupervised Learning and Preprocessing¶
Unsupervised learning subsumes all kinds of machine learning where there is no known output
In unsupervised learning, the learning algorithm is just shown the input data and asked to extract knowledge from this data.
Types of unsupervised learning¶
Two main types of unsupervised learning:
- Unsupervised transformations
- Clustering algorithms
Unsupervised transformations:¶
Unsupervised transformations of a dataset are algorithms that create a new representation of the data which might be easier for humans or other machine learning algorithms to understand compared to the original representation of the data
Unsupervised transformation application:
- Dimensionality reduction: takes a high-dimensional representation of the data, consisting of many features, and finds a new way to represent this data that summarizes the essential characteristics with fewer features.
- Finding the parts or components that “make up” the data. Ex: topic extraction
Clustering algorithms¶
Clustering algorithms, on the other hand, partition data into distinct groups of similar items.
Challenges in unsupervised learning¶
A major challenge in unsupervised learning is evaluating whether the algorithm learned something useful.
Unsupervised learning algorithms are usually applied to data that does not contain any label information, so we don’t know what the right output should be. Therefore, it is very hard to say whether a model “did well.”
As a consequence, Unsupervised algorithms are used often in an exploratory setting, when a data scientist wants to understand the data better, rather than as part of a larger automatic system.
Preprocessing and Scaling¶
The goal is to adjust the features so that the data representation is more suitable for these algorithms.
mglearn.plots.plot_scaling()
Different Kinds of Processing¶
- The Standard Scaler ensures that for each feature the mean is 0 and the variance is 1, bringing all features to the same magnitude. However, this scaling does not ensure any particular minimum and maximum values for the features.
- The RobustScaler works similarly to the StandardScaler in that it ensures statistical properties for each feature that guarantee that they are on the same scale.
- The RobustScaler uses the median and quartiles,1 instead of mean and variance. This makes the RobustScaler ignore data points that are very different from the rest (like measurement errors). These odd data points are also called outliers, and can lead to trouble for other scaling techniques.
- The MinMaxScaler, on the other hand, shifts the data such that all features are exactly between 0 and 1. For the two-dimensional dataset this means all of the data is contained within the rectangle created by the x-axis between 0 and 1 and the y-axis between 0 and 1.
- Finally, the Normalizer does a very different kind of rescaling. it projects a data point on the circle with a radius of 1.
Applying Data Transformations¶
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=1)
print(X_train.shape)
print(X_test.shape)
As a reminder, the dataset contains 569 data points, each represented by 30 measure ments. We split the dataset into 426 samples for the training set and 143 samples for the test set.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_train)
# transform data
X_train_scaled = scaler.transform(X_train)
# print dataset properties before and after scaling
print("transformed shape: {}".format(X_train_scaled.shape))
print("per-feature minimum before scaling:\n {}".format(X_train.min(axis=0)))
print("per-feature maximum before scaling:\n {}".format(X_train.max(axis=0)))
print("per-feature minimum after scaling:\n {}".format(
X_train_scaled.min(axis=0)))
print("per-feature maximum after scaling:\n {}".format(
X_train_scaled.max(axis=0)))
The transformed data has the same shape as the original data—the features are simply shifted and scaled.
# transform test data
X_test_scaled = scaler.transform(X_test)
# print test data properties after scaling
print("per-feature minimum after scaling:\n{}".format(X_test_scaled.min(axis=0)))
print("per-feature maximum after scaling:\n{}".format(X_test_scaled.max(axis=0)))
Scaling training and test data the same way¶
It is important to apply exactly the same transformation to the training set and the test set for the supervised model to work on the test set.
from sklearn.datasets import make_blobs
# make synthetic data
X, _ = make_blobs(n_samples=50, centers=5, random_state=4, cluster_std=2)
# split it into training and test sets
X_train, X_test = train_test_split(X, random_state=5, test_size=.1)
# plot the training and test sets
fig, axes = plt.subplots(1, 3, figsize=(13, 4))
axes[0].scatter(X_train[:, 0], X_train[:, 1],
c=mglearn.cm2(0), label="Training set", s=60)
axes[0].scatter(X_test[:, 0], X_test[:, 1], marker='^',
c=mglearn.cm2(1), label="Test set", s=60)
axes[0].legend(loc='upper left')
axes[0].set_title("Original Data")
# scale the data using MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# visualize the properly scaled data
axes[1].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
c=mglearn.cm2(0), label="Training set", s=60)
axes[1].scatter(X_test_scaled[:, 0], X_test_scaled[:, 1], marker='^',
c=mglearn.cm2(1), label="Test set", s=60)
axes[1].set_title("Scaled Data")
# rescale the test set separately
# so test set min is 0 and test set max is 1
# DO NOT DO THIS! For illustration purposes only.
test_scaler = MinMaxScaler()
test_scaler.fit(X_test)
X_test_scaled_badly = test_scaler.transform(X_test)
# visualize wrongly scaled data
axes[2].scatter(X_train_scaled[:, 0], X_train_scaled[:, 1],
c=mglearn.cm2(0), label="training set", s=60)
axes[2].scatter(X_test_scaled_badly[:, 0], X_test_scaled_badly[:, 1],
marker='^', c=mglearn.cm2(1), label="test set", s=60)
axes[2].set_title("Improperly Scaled Data")
for ax in axes:
ax.set_xlabel("Feature 0")
ax.set_ylabel("Feature 1")
fig.tight_layout()
- The first panel is an unscaled two-dimensional dataset
- The second panel is the same data, but scaled using the MinMaxScaler
- The third panel shows what would happen if we scaled the training set and test set separately. In this case, the minimum and maximum feature values for both the training and the test set are 0 and 1. But now the dataset looks different. The test points moved incongruously to the training set, as they were scaled differently
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
# calling fit and transform in sequence (using method chaining)
X_scaled = scaler.fit(X_train).transform(X_train)
# same result, but more efficient computation
X_scaled_d = scaler.fit_transform(X_train)
The effect of preprocessing on supervised learning¶
from sklearn.svm import SVC
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target,
random_state=0)
svm = SVC(C=100)
svm.fit(X_train, y_train)
print("Test set accuracy: {:.2f}".format(svm.score(X_test, y_test)))
Now, let’s scale the data using MinMaxScaler before fitting the SVC:
# preprocessing using 0-1 scaling
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# learning an SVM on the scaled training data
svm.fit(X_train_scaled, y_train)
# scoring on the scaled test set
print("Scaled test set accuracy: {:.2f}".format(
svm.score(X_test_scaled, y_test)))
# preprocessing using zero mean and unit variance scaling
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)
# learning an SVM on the scaled training data
svm.fit(X_train_scaled, y_train)
# scoring on the scaled test set
print("SVM test accuracy: {:.2f}".format(svm.score(X_test_scaled, y_test)))
2. Dimensionality Reduction, Feature Extraction and Manifold Learning¶
Principal Component Analysis (PCA)¶
- Principal Component Analysis (PCA) is an unsupervised, non-parametric statistical technique primarily used for dimensionality reduction in machine learning.
- High dimensionality means that the dataset has a large number of features. The primary problem associated with high-dimensionality in the machine learning field is model overfitting, which reduces the ability to generalize beyond the examples in the training set.
Principal component analysis is a method that rotates the dataset in a way such that the rotated features are statistically uncorrelated.
This rotation is often followed by selecting only a subset of the new features, according to how important they are for explaining the data.
mglearn.plots.plot_pca_illustration()
The algorithm proceeds by first finding the direction of maximum variance, labeled “Component 1.” This is the direction (or vector) in the data that contains most of the information, or in other words, the direction along which the features are most correlated with each other
Then, the algorithm finds the direction that contains the most information while being orthogonal (at a right angle) to the first direction.
The directions found using this process are called principal components, as they are the main directions of variance in the data.
This transformation is sometimes used to remove noise effects from the data or visualize what part of the information is retained using the principal components.
Applying PCA to the cancer dataset for visualization¶
fig, axes = plt.subplots(15, 2, figsize=(10, 20))
malignant = cancer.data[cancer.target == 0]
benign = cancer.data[cancer.target == 1]
ax = axes.ravel()
for i in range(30):
_, bins = np.histogram(cancer.data[:, i], bins=50)
ax[i].hist(malignant[:, i], bins=bins, color=mglearn.cm3(0), alpha=.5)
ax[i].hist(benign[:, i], bins=bins, color=mglearn.cm3(2), alpha=.5)
ax[i].set_title(cancer.feature_names[i])
ax[i].set_yticks(())
ax[0].set_xlabel("Feature magnitude")
ax[0].set_ylabel("Frequency")
ax[0].legend(["malignant", "benign"], loc="best")
fig.tight_layout()
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
scaler = StandardScaler()
scaler.fit(cancer.data)
X_scaled = scaler.transform(cancer.data)
from sklearn.decomposition import PCA
# keep the first two principal components of the data
pca = PCA(n_components=2)
# fit PCA model to beast cancer data
pca.fit(X_scaled)
# transform data onto the first two principal components
X_pca = pca.transform(X_scaled)
print("Original shape: {}".format(str(X_scaled.shape)))
print("Reduced shape: {}".format(str(X_pca.shape)))
# plot first vs. second principal component, colored by class
plt.figure(figsize=(8, 8))
mglearn.discrete_scatter(X_pca[:, 0], X_pca[:, 1], cancer.target)
plt.legend(cancer.target_names, loc="best")
plt.gca().set_aspect("equal")
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
It is important to note that PCA is an unsupervised method, and does not use any class information when finding the rotation. It simply looks at the correlations in the data.
print("PCA component shape: {}".format(pca.components_.shape))
A downside of PCA is that the two axes in the plot are often not very easy to interpret. The principal components correspond to directions in the original data, so they are combinations of the original features. However, these combinations are usually very complex, as we’ll see shortly
print("PCA components:\n{}".format(pca.components_))
plt.matshow(pca.components_, cmap='viridis')
plt.yticks([0, 1], ["First component", "Second component"])
plt.colorbar()
plt.xticks(range(len(cancer.feature_names)),
cancer.feature_names, rotation=60, ha='left')
plt.xlabel("Feature")
plt.ylabel("Principal components")
Eigenfaces for feature extraction¶
Another application of PCA that we mentioned earlier is feature extraction.
The idea behind feature extraction is that it is possible to find a representation of your data that is better suited to analysis than the raw representation you were given.
Images are made up of pixels, usually stored as red, green, and blue (RGB) intensities. Objects in images are usually made up of thousands of pixels, and only together are they meaningful.
We will give a very simple application of feature extraction on images using PCA, by working with face images from the Labeled Faces in the Wild dataset.
from sklearn.datasets import fetch_lfw_people
people = fetch_lfw_people(min_faces_per_person=20, resize=0.7)
image_shape = people.images[0].shape
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
for target, image, ax in zip(people.target, people.images, axes.ravel()):
ax.imshow(image)
ax.set_title(people.target_names[target])
print("people.images.shape: {}".format(people.images.shape))
print("Number of classes: {}".format(len(people.target_names)))
# count how often each target appears
counts = np.bincount(people.target)
# print counts next to target names:
for i, (count, name) in enumerate(zip(counts, people.target_names)):
print("{0:25} {1:3}".format(name, count), end=' ')
if (i + 1) % 3 == 0:
print()
To make the data less skewed, we will only take up to 50 images of each person
mask = np.zeros(people.target.shape, dtype=np.bool)
for target in np.unique(people.target):
mask[np.where(people.target == target)[0][:50]] = 1
X_people = people.data[mask]
y_people = people.target[mask]
# scale the grey-scale values to be between 0 and 1
# instead of 0 and 255 for better numeric stability:
X_people = X_people / 255.
A simple solution is to use a one-nearest-neighbor classifier that looks for the most similar face image to the face you are classifying. This classifier could in principle work with only a single training example per class.
from sklearn.neighbors import KNeighborsClassifier
# split the data in training and test set
X_train, X_test, y_train, y_test = train_test_split(
X_people, y_people, stratify=y_people, random_state=0)
# build a KNeighborsClassifier with using one neighbor:
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print("Test set score of 1-nn: {:.2f}".format(knn.score(X_test, y_test)))
mglearn.plots.plot_pca_whitening()
pca = PCA(n_components=100, whiten=True, random_state=0).fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print("X_train_pca.shape: {}".format(X_train_pca.shape))
This is where PCA comes in. Computing distances in the original pixel space is quite a bad way to measure similarity between faces.
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train_pca, y_train)
print("Test set accuracy: {:.2f}".format(knn.score(X_test_pca, y_test)))
print("pca.components_.shape: {}".format(pca.components_.shape))
fig, axes = plt.subplots(3, 5, figsize=(15, 12),
subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(pca.components_, axes.ravel())):
ax.imshow(component.reshape(image_shape),
cmap='viridis')
ax.set_title("{}. component".format((i + 1)))
# FIXME hide this!
from matplotlib.offsetbox import OffsetImage, AnnotationBbox
image_shape = people.images[0].shape
plt.figure(figsize=(20, 3))
ax = plt.gca()
imagebox = OffsetImage(people.images[0], zoom=7, cmap="gray")
ab = AnnotationBbox(imagebox, (.05, 0.4), pad=0.0, xycoords='data')
ax.add_artist(ab)
for i in range(4):
imagebox = OffsetImage(pca.components_[i].reshape(image_shape), zoom=7,
cmap="viridis")
ab = AnnotationBbox(imagebox, (.3 + .2 * i, 0.4),
pad=0.0,
xycoords='data'
)
ax.add_artist(ab)
if i == 0:
plt.text(.18, .25, 'x_{} *'.format(i), fontdict={'fontsize': 50})
else:
plt.text(.15 + .2 * i, .25, '+ x_{} *'.format(i),
fontdict={'fontsize': 50})
plt.text(.95, .25, '+ ...', fontdict={'fontsize': 50})
plt.text(.13, .3, r'\approx', fontdict={'fontsize': 50})
plt.axis("off")
plt.savefig("images/03-face_decomposition.png")
plt.close()
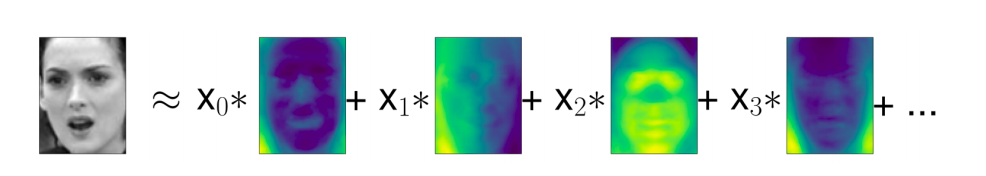
mglearn.plots.plot_pca_faces(X_train, X_test, image_shape)
mglearn.discrete_scatter(X_train_pca[:, 0], X_train_pca[:, 1], y_train)
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
Non-Negative Matrix Factorization (NMF)¶
- In PCA we wanted components that were orthogonal and that explained as much variance of the data as possible.
- In NMF, we want the components and the coefficients to be nonnegative; that is, we want both the components and the coefficients to be greater than or equal to zero. Consequently, this method can only be applied to data where each feature is non-negative, as a non-negative sum of non-negative components cannot become negative.
The process of decomposing data into a non-negative weighted sum is particularly helpful for data that is created as the addition (or overlay) of several independent sources, such as an audio track of multiple people speaking, or music with many instruments. => In these situations, NMF can identify the original components that make up the combined data.
NMF leads to more interpretable (explainable) components than PCA, as negative components and coefficients can lead to hard-to-interpret cancellation effects.
Applying NMF to synthetic data¶
mglearn.plots.plot_nmf_illustration()
Applying NMF to face images¶
mglearn.plots.plot_nmf_faces(X_train, X_test, image_shape)
from sklearn.decomposition import NMF
nmf = NMF(n_components=15, random_state=0)
nmf.fit(X_train)
X_train_nmf = nmf.transform(X_train)
X_test_nmf = nmf.transform(X_test)
fig, axes = plt.subplots(3, 5, figsize=(15, 12),
subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(nmf.components_, axes.ravel())):
ax.imshow(component.reshape(image_shape))
ax.set_title("{}. component".format(i))
compn = 3
# sort by 3rd component, plot first 10 images
inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
fig.suptitle("Large component 3")
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
ax.imshow(X_train[ind].reshape(image_shape))
compn = 7
# sort by 7th component, plot first 10 images
inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig.suptitle("Large component 7")
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
subplot_kw={'xticks': (), 'yticks': ()})
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
ax.imshow(X_train[ind].reshape(image_shape))
S = mglearn.datasets.make_signals()
plt.figure(figsize=(6, 1))
plt.plot(S, '-')
plt.xlabel("Time")
plt.ylabel("Signal")
# Mix data into a 100 dimensional state
A = np.random.RandomState(0).uniform(size=(100, 3))
X = np.dot(S, A.T)
print("Shape of measurements: {}".format(X.shape))
nmf = NMF(n_components=3, random_state=42)
S_ = nmf.fit_transform(X)
print("Recovered signal shape: {}".format(S_.shape))
pca = PCA(n_components=3)
H = pca.fit_transform(X)
models = [X, S, S_, H]
names = ['Observations (first three measurements)',
'True sources',
'NMF recovered signals',
'PCA recovered signals']
fig, axes = plt.subplots(4, figsize=(8, 4), gridspec_kw={'hspace': .5},
subplot_kw={'xticks': (), 'yticks': ()})
for model, name, ax in zip(models, names, axes):
ax.set_title(name)
ax.plot(model[:, :3], '-')
Manifold Learning with t-SNE¶
from sklearn.datasets import load_digits
digits = load_digits()
fig, axes = plt.subplots(2, 5, figsize=(10, 5),
subplot_kw={'xticks':(), 'yticks': ()})
for ax, img in zip(axes.ravel(), digits.images):
ax.imshow(img)
# build a PCA model
pca = PCA(n_components=2)
pca.fit(digits.data)
# transform the digits data onto the first two principal components
digits_pca = pca.transform(digits.data)
colors = ["#476A2A", "#7851B8", "#BD3430", "#4A2D4E", "#875525",
"#A83683", "#4E655E", "#853541", "#3A3120", "#535D8E"]
plt.figure(figsize=(10, 10))
plt.xlim(digits_pca[:, 0].min(), digits_pca[:, 0].max())
plt.ylim(digits_pca[:, 1].min(), digits_pca[:, 1].max())
for i in range(len(digits.data)):
# actually plot the digits as text instead of using scatter
plt.text(digits_pca[i, 0], digits_pca[i, 1], str(digits.target[i]),
color = colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("First principal component")
plt.ylabel("Second principal component")
from sklearn.manifold import TSNE
tsne = TSNE(random_state=42)
# use fit_transform instead of fit, as TSNE has no transform method
digits_tsne = tsne.fit_transform(digits.data)
plt.figure(figsize=(10, 10))
plt.xlim(digits_tsne[:, 0].min(), digits_tsne[:, 0].max() + 1)
plt.ylim(digits_tsne[:, 1].min(), digits_tsne[:, 1].max() + 1)
for i in range(len(digits.data)):
# actually plot the digits as text instead of using scatter
plt.text(digits_tsne[i, 0], digits_tsne[i, 1], str(digits.target[i]),
color = colors[digits.target[i]],
fontdict={'weight': 'bold', 'size': 9})
plt.xlabel("t-SNE feature 0")
plt.ylabel("t-SNE feature 1")
3. Clustering¶
- Clustering is the task of partitioning the dataset into groups
k-Means clustering¶
- K-mean tries to find cluster centers that are representative of certain regions of the data.
- The algorithm alternates between two steps:
- Assigning each data point to the closest cluster center
- Setting each cluster center as the mean of the data points that are assigned to it.
- The algorithm is finished when the assignment of instances to clusters no longer changes.
mglearn.plots.plot_kmeans_algorithm()
mglearn.plots.plot_kmeans_boundaries()
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# generate synthetic two-dimensional data
X, y = make_blobs(random_state=1)
# build the clustering model
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
print("Cluster memberships:\n{}".format(kmeans.labels_))
print(kmeans.predict(X))
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o')
mglearn.discrete_scatter(
kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2],
markers='^', markeredgewidth=2)
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
# using two cluster centers:
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
assignments = kmeans.labels_
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignments, ax=axes[0])
# using five cluster centers:
kmeans = KMeans(n_clusters=5)
kmeans.fit(X)
assignments = kmeans.labels_
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignments, ax=axes[1])
Failure cases of k-Means¶
Even if you know the “right” number of clusters for a given dataset, k-means might not always be able to recover them. Each cluster is defined solely by its center, which means that each cluster is a convex shape.
As a result of this, k-means can only capture relatively simple shapes. k-means also assumes that all clusters have the same “diameter” in some sense; it always draws the boundary between clusters to be exactly in the middle between the cluster centers.
X_varied, y_varied = make_blobs(n_samples=200,
cluster_std=[1.0, 2.5, 0.5],
random_state=170)
y_pred = KMeans(n_clusters=3, random_state=0).fit_predict(X_varied)
mglearn.discrete_scatter(X_varied[:, 0], X_varied[:, 1], y_pred)
plt.legend(["cluster 0", "cluster 1", "cluster 2"], loc='best')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
# generate some random cluster data
X, y = make_blobs(random_state=170, n_samples=600)
rng = np.random.RandomState(74)
# transform the data to be stretched
transformation = rng.normal(size=(2, 2))
X = np.dot(X, transformation)
# cluster the data into three clusters
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
y_pred = kmeans.predict(X)
# plot the cluster assignments and cluster centers
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o')
mglearn.discrete_scatter(
kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2],
markers='^', markeredgewidth=2)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
As k-means only considers the distance to the nearest cluster center, it can’t handle this kind of data as above.
# generate synthetic two_moons data (with less noise this time)
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# cluster the data into two clusters
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
y_pred = kmeans.predict(X)
# plot the cluster assignments and cluster centers
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap=mglearn.cm2, s=60, edgecolor='k')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', c=[mglearn.cm2(0), mglearn.cm2(1)], s=100, linewidth=2,
edgecolor='k')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
k-means also performs poorly if the clusters have more complex shapes as mention above
Vector Quantization - Or Seeing k-Means as Decomposition¶
X_train, X_test, y_train, y_test = train_test_split(
X_people, y_people, stratify=y_people, random_state=0)
nmf = NMF(n_components=100, random_state=0)
nmf.fit(X_train)
pca = PCA(n_components=100, random_state=0)
pca.fit(X_train)
kmeans = KMeans(n_clusters=100, random_state=0)
kmeans.fit(X_train)
X_reconstructed_pca = pca.inverse_transform(pca.transform(X_test))
X_reconstructed_kmeans = kmeans.cluster_centers_[kmeans.predict(X_test)]
X_reconstructed_nmf = np.dot(nmf.transform(X_test), nmf.components_)
fig, axes = plt.subplots(3, 5, figsize=(8, 8),
subplot_kw={'xticks': (), 'yticks': ()})
fig.suptitle("Extracted Components")
for ax, comp_kmeans, comp_pca, comp_nmf in zip(
axes.T, kmeans.cluster_centers_, pca.components_, nmf.components_):
ax[0].imshow(comp_kmeans.reshape(image_shape))
ax[1].imshow(comp_pca.reshape(image_shape), cmap='viridis')
ax[2].imshow(comp_nmf.reshape(image_shape))
axes[0, 0].set_ylabel("kmeans")
axes[1, 0].set_ylabel("pca")
axes[2, 0].set_ylabel("nmf")
fig, axes = plt.subplots(4, 5, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(8, 8))
fig.suptitle("Reconstructions")
for ax, orig, rec_kmeans, rec_pca, rec_nmf in zip(
axes.T, X_test, X_reconstructed_kmeans, X_reconstructed_pca,
X_reconstructed_nmf):
ax[0].imshow(orig.reshape(image_shape))
ax[1].imshow(rec_kmeans.reshape(image_shape))
ax[2].imshow(rec_pca.reshape(image_shape))
ax[3].imshow(rec_nmf.reshape(image_shape))
axes[0, 0].set_ylabel("original")
axes[1, 0].set_ylabel("kmeans")
axes[2, 0].set_ylabel("pca")
axes[3, 0].set_ylabel("nmf")
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
kmeans = KMeans(n_clusters=10, random_state=0)
kmeans.fit(X)
y_pred = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=60, cmap='Paired')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=60,
marker='^', c=range(kmeans.n_clusters), linewidth=2, cmap='Paired')
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
print("Cluster memberships:\n{}".format(y_pred))
distance_features = kmeans.transform(X)
print("Distance feature shape: {}".format(distance_features.shape))
print("Distance features:\n{}".format(distance_features))
Agglomerative Clustering¶
mglearn.plots.plot_agglomerative_algorithm()
from sklearn.cluster import AgglomerativeClustering
X, y = make_blobs(random_state=1)
agg = AgglomerativeClustering(n_clusters=3)
assignment = agg.fit_predict(X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignment)
plt.legend(["Cluster 0", "Cluster 1", "Cluster 2"], loc="best")
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
Hierarchical Clustering and Dendrograms¶
mglearn.plots.plot_agglomerative()
# Import the dendrogram function and the ward clustering function from SciPy
from scipy.cluster.hierarchy import dendrogram, ward
X, y = make_blobs(random_state=0, n_samples=12)
# Apply the ward clustering to the data array X
# The SciPy ward function returns an array that specifies the distances
# bridged when performing agglomerative clustering
linkage_array = ward(X)
# Now we plot the dendrogram for the linkage_array containing the distances
# between clusters
dendrogram(linkage_array)
# mark the cuts in the tree that signify two or three clusters
ax = plt.gca()
bounds = ax.get_xbound()
ax.plot(bounds, [7.25, 7.25], '--', c='k')
ax.plot(bounds, [4, 4], '--', c='k')
ax.text(bounds[1], 7.25, ' two clusters', va='center', fontdict={'size': 15})
ax.text(bounds[1], 4, ' three clusters', va='center', fontdict={'size': 15})
plt.xlabel("Sample index")
plt.ylabel("Cluster distance")
DBSCAN¶
Another very useful clustering algorithm is DBSCAN (which stands for “densitybased spatial clustering of applications with noise”).
- The main benefits of DBSCAN are that it does not require the user to set the number of clusters a priori, it can capture clusters of complex shapes, and it can identify points that are not part of any cluster.
- DBSCAN is somewhat slower than agglomerative clustering and k-means, but still scales to relatively large datasets.
from sklearn.cluster import DBSCAN
X, y = make_blobs(random_state=0, n_samples=12)
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X)
print("Cluster memberships:\n{}".format(clusters))
mglearn.plots.plot_dbscan()
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# Rescale the data to zero mean and unit variance
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
dbscan = DBSCAN()
clusters = dbscan.fit_predict(X_scaled)
# plot the cluster assignments
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm2, s=60)
plt.xlabel("Feature 0")
plt.ylabel("Feature 1")
DBSCAN works by identifying points that are in “crowded” regions of the feature space, where many data points are close together. These regions are referred to as dense regions in feature space.
The idea behind DBSCAN is that clusters form dense regions of data, separated by regions that are relatively empty.
Points that are within a dense region are called core samples
There are two parameters in DBSCAN: min_samples and eps.
- If there are at least min_samples many data points within a distance of eps to a given data point, that data point is classified as a core sample.
- Core samples that are closer to each other than the distance eps are put into the same cluster by DBSCAN.
How to build DBSCAN?¶
- Picking an arbitrary point to start
- It then finds all points with distance eps or less from that point.
- If there are less than min_samples points within distance eps of the starting point, this point is labeled as noise, meaning that it doesn’t belong to any cluster.
- If there are more than min_samples points within a distance of eps, the point is labeled a core sample and assigned a new cluster label.
- Then, all neighbors (within eps) of the point are visited.
- If they have not been assigned a cluster yet, they are assigned the new cluster label that was just created.
- If they are core samples, their neighbors are visited in turn, and so on.
- The cluster grows until there are no more core samples within distance eps of the cluster. Then another point that hasn’t yet been visited is picked, and the same procedure is repeated.
- In the end, there are three kinds of points:
- core points
- points that are within distance eps of core points (called boundary points)
- noise.
When the DBSCAN algorithm is run on a particular dataset multiple times, the clustering of the core points is always the same, and the same points will always be labeled as noise.
Comparing and evaluating clustering algorithms¶
One of the challenges in applying clustering algorithms is that it is very hard to assess how well an algorithm worked, and to compare outcomes between different algorithms. After talking about the algorithms behind k-means, agglomerative clustering, and DBSCAN
Evaluating clustering with ground truth¶
There are metrics that can be used to assess the outcome of a clustering algorithm relative to a ground truth clustering, the most important ones being the adjusted rand index (ARI) and normalized mutual information (NMI), which both provide a quantitative measure between 0 and 1.
from sklearn.metrics.cluster import adjusted_rand_score
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# Rescale the data to zero mean and unit variance
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
fig, axes = plt.subplots(1, 4, figsize=(15, 3),
subplot_kw={'xticks': (), 'yticks': ()})
# make a list of algorithms to use
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2),
DBSCAN()]
# create a random cluster assignment for reference
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(X))
# plot random assignment
axes[0].scatter(X_scaled[:, 0], X_scaled[:, 1], c=random_clusters,
cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment - ARI: {:.2f}".format(
adjusted_rand_score(y, random_clusters)))
for ax, algorithm in zip(axes[1:], algorithms):
# plot the cluster assignments and cluster centers
clusters = algorithm.fit_predict(X_scaled)
ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters,
cmap=mglearn.cm3, s=60)
ax.set_title("{} - ARI: {:.2f}".format(algorithm.__class__.__name__,
adjusted_rand_score(y, clusters)))
from sklearn.metrics import accuracy_score
# these two labelings of points correspond to the same clustering
clusters1 = [0, 0, 1, 1, 0]
clusters2 = [1, 1, 0, 0, 1]
# accuracy is zero, as none of the labels are the same
print("Accuracy: {:.2f}".format(accuracy_score(clusters1, clusters2)))
# adjusted rand score is 1, as the clustering is exactly the same:
print("ARI: {:.2f}".format(adjusted_rand_score(clusters1, clusters2)))
Evaluating clustering without ground truth¶
from sklearn.metrics.cluster import silhouette_score
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# rescale the data to zero mean and unit variance
scaler = StandardScaler()
scaler.fit(X)
X_scaled = scaler.transform(X)
fig, axes = plt.subplots(1, 4, figsize=(15, 3),
subplot_kw={'xticks': (), 'yticks': ()})
# create a random cluster assignment for reference
random_state = np.random.RandomState(seed=0)
random_clusters = random_state.randint(low=0, high=2, size=len(X))
# plot random assignment
axes[0].scatter(X_scaled[:, 0], X_scaled[:, 1], c=random_clusters,
cmap=mglearn.cm3, s=60)
axes[0].set_title("Random assignment: {:.2f}".format(
silhouette_score(X_scaled, random_clusters)))
algorithms = [KMeans(n_clusters=2), AgglomerativeClustering(n_clusters=2),
DBSCAN()]
for ax, algorithm in zip(axes[1:], algorithms):
clusters = algorithm.fit_predict(X_scaled)
# plot the cluster assignments and cluster centers
ax.scatter(X_scaled[:, 0], X_scaled[:, 1], c=clusters, cmap=mglearn.cm3,
s=60)
ax.set_title("{} : {:.2f}".format(algorithm.__class__.__name__,
silhouette_score(X_scaled, clusters)))
Comparing algorithms on the faces dataset¶
# extract eigenfaces from lfw data and transform data
from sklearn.decomposition import PCA
pca = PCA(n_components=100, whiten=True, random_state=0)
X_pca = pca.fit_transform(X_people)
Analyzing the faces dataset with DBSCAN¶
# apply DBSCAN with default parameters
dbscan = DBSCAN()
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))
dbscan = DBSCAN(min_samples=3)
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))
dbscan = DBSCAN(min_samples=3, eps=15)
labels = dbscan.fit_predict(X_pca)
print("Unique labels: {}".format(np.unique(labels)))
# count number of points in all clusters and noise.
# bincount doesn't allow negative numbers, so we need to add 1.
# the first number in the result corresponds to noise points
print("Number of points per cluster: {}".format(np.bincount(labels + 1)))
noise = X_people[labels==-1]
fig, axes = plt.subplots(3, 9, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(12, 4))
for image, ax in zip(noise, axes.ravel()):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
for eps in [1, 3, 5, 7, 9, 11, 13]:
print("\neps={}".format(eps))
dbscan = DBSCAN(eps=eps, min_samples=3)
labels = dbscan.fit_predict(X_pca)
print("Number of clusters: {}".format(len(np.unique(labels))))
print("Cluster sizes: {}".format(np.bincount(labels + 1)))
dbscan = DBSCAN(min_samples=3, eps=7)
labels = dbscan.fit_predict(X_pca)
for cluster in range(max(labels) + 1):
mask = labels == cluster
n_images = np.sum(mask)
fig, axes = plt.subplots(1, n_images, figsize=(n_images * 1.5, 4),
subplot_kw={'xticks': (), 'yticks': ()})
for image, label, ax in zip(X_people[mask], y_people[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title(people.target_names[label].split()[-1])
Analyzing the faces dataset with k-Means¶
# extract clusters with k-Means
km = KMeans(n_clusters=10, random_state=0)
labels_km = km.fit_predict(X_pca)
print("Cluster sizes k-means: {}".format(np.bincount(labels_km)))
fig, axes = plt.subplots(2, 5, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(12, 4))
for center, ax in zip(km.cluster_centers_, axes.ravel()):
ax.imshow(pca.inverse_transform(center).reshape(image_shape),
vmin=0, vmax=1)
mglearn.plots.plot_kmeans_faces(km, pca, X_pca, X_people,
y_people, people.target_names)
Analyzing the faces dataset with agglomerative clustering¶
# extract clusters with ward agglomerative clustering
agglomerative = AgglomerativeClustering(n_clusters=10)
labels_agg = agglomerative.fit_predict(X_pca)
print("cluster sizes agglomerative clustering: {}".format(
np.bincount(labels_agg)))
print("ARI: {:.2f}".format(adjusted_rand_score(labels_agg, labels_km)))
linkage_array = ward(X_pca)
# now we plot the dendrogram for the linkage_array
# containing the distances between clusters
plt.figure(figsize=(20, 5))
dendrogram(linkage_array, p=7, truncate_mode='level', no_labels=True)
plt.xlabel("Sample index")
plt.ylabel("Cluster distance")
n_clusters = 10
for cluster in range(n_clusters):
mask = labels_agg == cluster
fig, axes = plt.subplots(1, 10, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(15, 8))
axes[0].set_ylabel(np.sum(mask))
for image, label, asdf, ax in zip(X_people[mask], y_people[mask],
labels_agg[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title(people.target_names[label].split()[-1],
fontdict={'fontsize': 9})
# extract clusters with ward agglomerative clustering
agglomerative = AgglomerativeClustering(n_clusters=40)
labels_agg = agglomerative.fit_predict(X_pca)
print("cluster sizes agglomerative clustering: {}".format(np.bincount(labels_agg)))
n_clusters = 40
for cluster in [10, 13, 19, 22, 36]: # hand-picked "interesting" clusters
mask = labels_agg == cluster
fig, axes = plt.subplots(1, 15, subplot_kw={'xticks': (), 'yticks': ()},
figsize=(15, 8))
cluster_size = np.sum(mask)
axes[0].set_ylabel("#{}: {}".format(cluster, cluster_size))
for image, label, asdf, ax in zip(X_people[mask], y_people[mask],
labels_agg[mask], axes):
ax.imshow(image.reshape(image_shape), vmin=0, vmax=1)
ax.set_title(people.target_names[label].split()[-1],
fontdict={'fontsize': 9})
for i in range(cluster_size, 15):
axes[i].set_visible(False)
Summary of Clustering Methods¶
Each of the algorithms has somewhat different strengths.
- k-means allows for a characterization of the clusters using the cluster means. It can also be viewed as a decomposition method, where each data point is represented by its cluster center.
- DBSCAN allows for the detection of “noise points” that are not assigned any cluster, and it can help automatically determine the number of clusters
Summary and Outlook¶
Decomposition, manifold learning, and clustering are essential tools to further your understanding of your data, and can be the only ways to make sense of your data in the absence of supervision information.
Often it is hard to quantify the usefulness of an unsupervised algorithm, though this shouldn’t deter you from using them to gather insights from your data.
from sklearn.linear_model import LogisticRegression
logreg = LogisticRegression()

Comments !